形式と構造のことばとしての「数学」
数学とはことばの世界である、などというようなことを前回の記事でかなり強く主張したわけだけれども、じゃあぼくが数学をどれほど理解しているのかというのはまったく別の問題になる。
乏しい知識で語っちゃう浅はかさをお許しいただきたいのだが、20世紀は数学にとって激動の時代だった。なかでももっとも広く知られ、数学の範疇さえこえて多大な影響をおよぼしたのがクルト・ゲーテルの「不完全性定理」だろう。
不完全性定理の発端となるのはダフィット・ヒルベルトによる「数学という体系そのものを数学しよう」という試みだった。ヒルベルトは19世紀後半から20世紀前半にかけて活躍した大数学者で、「無限ホテルのパラドックス」という無限と有限の概念に関するこれまた有名な思考実験でも知られているのだが、この件に関してもパラドックスが重要なテーマとなっている。
ヒルベルト自身は数学の完全性を信じていて、「適切な公理さえ設定されれば、そのシステム(=数学)全体は無矛盾である」と考えていた。公理に基づく推論は必ず矛盾を起こすことなく説明可能だという立場をとったこのアイデアに一石を投じたのがまさしくゲーデルの「不完全性定理」だった。
ざっくりと噛み砕いて説明すると、『「数学」という形式そのものを引数として、それ自身の形式でどれだけ推論を進めてみても、自らの無矛盾性は証明できない』という感じになる。この定理をめぐって同時代の偉大な数学者を複数巻き込んだ物語があるのだが、それはここでは割愛させていただく。
そして後年、計算機科学の大家アラン・チューリングによって「チューリング・マシン」が考案された。これを用いて行われた「停止問題」では、プログラミングが一般化した現代のことばに置き換えると、『あるプログラムのバグの有無を判定するプログラムは存在しない』という感じになる。プログラミングなどしていると、「書いたプログラムが間違っていたら自動修正してくれるプログラムとか組み込めたら楽なのになー」みたいなことをよくおもうのだが、停止問題により導かれたこの結果はゲーテルの不完全性定理と一致するものだといわれている。
長々と「数学」という形式についての話をしたのだが、「数学を数学する」といったように、20世紀ではこうした「メタ化」が学問領域を超えて盛んに行われた気がする。
たとえば文学において、ことばそのものを主題にした表現や、小説そのものを小説の題材にしようとする表現が、ダダイズム、シュールレアリスム、ポストモダン文学、ウリポ、ヌーヴォーロマンなどさまざまな呼び名が与えられたものたちによって積極的に扱われている。これらが統一的な見解を見出したかどうかを述べるのは容易いことではないが、しかし「難問」とされるものは形式と構造に孕む問題意識から生じていると考えられるのではないだろうか?
「数学そのもののことば」を身につけなければ題意すらわからない「ミレニアム懸賞問題」
さて、以上で20世紀の数学の難問についての一例を駆け足(というよりも爆速)でふりかえってみたのだが、かつてヒルベルトが重要難問を23題をざっとリストアップしたように、2000年にクレイ数学研究所が現代の難問として7題をリストアップした。いわゆる「ミレニアム懸賞問題」というやつで、解いたら賞金100万ドルが与えられる。その7題を以下に列挙する。
1:ヤン-ミルズ方程式と質量ギャップ問題
2:リーマン予想
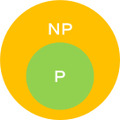
3:P≠NP予想
4:ナビエ-ストークス方程式の解の存在と滑らかさ
5:ホッジ予想
6:ポアンカレ予想
7:バーチ・スウィンナートン=ダイアー予想(BSD予想)
聞いたことのあるものからピンとこないものもいろいろあるんじゃないかとおもう。
このなかでも特に「ポアンカレ予想」がグリゴリー・ペレルマンにより解決されたのは有名で、さらにこの業績によってペレルマンは2006年に数学のノーベル賞ともいわれる「フィールズ賞」に選ばれたが、当人が受賞を拒否したという話もあり、なおいっそうの話題を呼んだ。他にもリーマン予想あたりは数学を題材としたフィクション作品でもよく取り上げられるため「名前だけでも聞いたことがある」という方が多いかとおもう。
この記事では、「それぞれがどのような問題なのか」の解説を行うつもりはない。というか、それはぼくの力量では不可能だからだ。
以前、こんな事があった。ぼくの友人でロシア文学の研究者がいるのだけれど、かれの研究対象としている文学作品にはとある数学概念を有するものがあった。友人は作品分析のために数学の文献を漁ったのだが、そこに書かれている数式を読み解けず、たまたま居合わせたぼくに解説を要求した。しかし、ぼくは断った。パッと読んだところでわかるはずがないのである。しかし断るからには言い訳が必要で、そのときぼくは、「ぼくは英語は読めるけれど、ラテン語は読めないから勘弁してくれ」といった。
ぼくは工学部出身の人間だ。数学は研究で散々使ってはきたけれど、「数学そのもの」については耳学問程度の知識しかない。そして「数学そのもの」の研究にはその分野のことばが使われていて、工学部(あるいは物理系)の人間からみれば見知らぬ外国語だ。例えばホッジ予想はこのように文章化されている。
複素解析多様体のあるホモロジー類は、代数的なド・ラームコホモロジー類であろう、つまり、部分多様体のホモロジー類のポアンカレ双対の和として表されるようなド・ラームコホモロジー類であろう。
ミレニアム懸賞問題 - Wikipedeia
代数幾何学の素養のないぼくにとって、この文章は単語レベルでなにがどういうことなのかを理解することができない。情けない話だが、それゆえになにがどう難しくて、どのような点で重要な問題なのか、いくら説明を聞いても理解できない。かつて西洋ではラテン語のリテラシーがなければ学問ができなかったように、数学を本気で深いところでやるためには「数学そのもの」のことばのリテラシーがなければならない。上に引用した文章がなんなのかを理解するためには、言語的素養が必要になる。
工学系に馴染み深い問題
しかし、「ミレニアム懸賞問題って意味わかんないよねー」という話で終わってしまってはこの記事の意味というものがなくなってしまう。ミレニアム懸賞問題は純粋数学の他、物理学などにとっても重要なものを扱っていて、特に「ナビエ-ストークス方程式の解の安定性と滑らかさ」と「P≠NP予想」については工学的な要素があり、比較的具体的な問題として捉えやすい。
「ナビエ-ストークス方程式」とは流体力学で極めて重要なものであり、工学部機械工学科の学生であれば学部初年度から必修科目として履修することになるものだ。この方程式により流体がどのように流れるのかを計算することが可能で、実際に代表的な数値シミュレーションとして大学や企業を問わず幅広く活用されている。
■参考動画
しかしこの方程式、歴史そのものは古いのだがその解の性質について、つまり紙とペンで行う手計算については、わかっていないことが多くある。流れの研究を難しくしているのが「乱流」という不安定ないわゆる「カオス現象」なのだが、ナビエ-ストークス方程式の一般解がもしあるとするならば、乱流の構造に解析的な理解が与えられることになる。この問題は「そもそもそんな解が存在するのか?」ということである。
もうひとつ工学系に馴染み深いものとしてあげられるのが「P≠NP予想」だ。
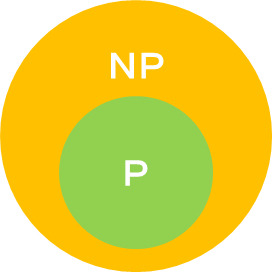
これは計算機工学にとって重要な問題であり、ひとことでいうならば「任意の問題は手計算で解くことが可能か?」というもので、「解ける/解けない」に関係している。ここでは数学的な問題がPとNPに分類されていて、Pは「手計算でバチッと解ける問題」で、NPは「対象となるデータをしらみつぶしにしないと解けない問題」になる。
コンピューターが使用されるようになり、その圧倒的な処理能力により多くの問題が「解かれて」きたのはいうまでもなく、先に挙げた現在の数値流体シミュレーションも例に漏れずその恩恵を受けている。しかし、大きな問題として「解ける」といっても「どれくらいの時間で」というのが重要になってきた。
流体シミュレーションにしろ分子シミュレーションにしろ、コンピューターを使ってゴリゴリ愚直に計算していけば、どんなに大きな系であっても無限時間経てば「解ける」。しかし、現実的なことを考えると問題は有限時間内に解けなければ意味がない。それゆえに膨大なデータにより構成される系の計算では、効率的に解けるアルゴリズムの構築が不可欠となる。P=NPとは「どんな問題でも効率的に解けるアルゴリズムが存在する」ということなのだが、一般的にこれらは等号ではないと考えられている。しかし、その数学的な証明が現状ではなされていない。
「効率的なアルゴリズムを探す」という研究は多数あり、それは「巡回セールスマン問題」という名前で知られている。アメリカの各州を回る営業マンの最短ルートを探し出す方法を問う問題であるが、これを効率的に解く手法は現在進行形で世界中で研究されている。
■参考動画
例に挙げた動画は、「ブランコの最適な漕ぎ方を見つけるシミュレーション」だ。選択肢が非常に多いもののなかから最適解をしらみつぶしに探すのは宇宙を何回もやり直すくらい時間がかかるものだが、動画では「遺伝的アルゴリズム」という手法を用いてうまく効率化している。これは名前の通り遺伝学の発想を取り入れたもので、「評価する数値が高いものを組み合わせていくことで最大値を見つけましょう」というアルゴリズムだ。
ともあれ「解ける」ということの意味が問われるようになると、「問題の構造」についての議論が避けられなくなる。そしてその構造は数学という言語で分析されているのか、はたまた人間よりも先に存在していた数学によりあらかじめ織り成されていたものなのか、その体系に組み込まれてしまっているぼくたちにはわかりえない。ひとまずか、あるいは、原理的にか。
※「発想」はどこからやってくるのか……羽生善治の「大局観」とAIによる「演算処理」

【著者】まちゃひこ
京都大学大学院に在学中、日本学術振興会(JSPS)特別研究員やカーネギーメロン大学への客員研究員としての留学を経験。博士課程を単位取得中退後、いろいろあって広告代理店の営業職として就職。そしてまたいろいろあってフリーライターとなる。文芸作品のレビューや自然科学のコラムを中心に書いている他、創作プロジェクト「大滝瓶太」を主宰し、小説の創作や翻訳を行っている。電子書籍レーベル「惑星と口笛ブックス」より短篇集『コロニアルタイム』を2017年に発表。読書中心のブログ『カプリスのかたちをしたアラベスク』やTwitter(@macha_hiko)でも発信中。
■読書中心のブログ『カプリスのかたちをしたアラベスク』http://www.waka-macha.com/
■Twitter https://twitter.com/macha_hiko