
BtoB情報検索サイト「イプロス」「イプロスものづくり」を運営する株式会社イプロス(本社:東京都港区)は、「建築構造力学」の知識資料の第1章を公開しました。
<もくじ>
1. 力とは
2. 建築構造物のモデル化
3. 単純梁と片持ち梁の反力計算
4. 応力とは
5. 静定梁の応力計算
6. 静定トラスの応力計算
7. 不静定問題を解くためには
資料DLはこちら
※ログインが必要です。登録状況により新規会員登録が必要な場合があります。
「建築構造力学の基礎知識」
建築構造力学の世界へようこそ。私たちの祖先は太古の時代から、我が身を守るために住む空間を築いてきました。
また、時代の移り変わりとともに社会活動が広がると、より大きく、より頑丈な建造物が必要とされました。建築構造力学は、安全で安心な建築構造物を築くための技術の根幹をなす学問です。
本連載では、全7回にわたり建築構造力学の基礎知識を紹介します。
第1回は、力について解説します。
<第1回 もくじ>
1. 力と力の表し方
2. 力の合成と分解
3. モーメント
1. 力と力の表し方
力とは、物体の静止あるいは運動している状態に変化を起こさせたり、物体に変形を生じさせたりする作用をいいます。静止している物体に力を加えると、物体は動き始めます。質量1kgの物体に対し、加速度1m/sec2を与えるのに必要な力を1N(ニュートン)といいます。
地球上にある物体は、重力によって常にg=9.8m/sec2を受けます。
例えば、質量60kgの人は、60×9.8=588Nの力を受けています。
これは構造物にとっても同じことです。質量mの構造物は、常に地球からmgの力を受けています。
力を表示するには、力の大きさ、力の方向、力の作用点の3つが必要です。
これらを力の三要素といいます。力を図で表すと、矢印で表示することができます(図1)。
このとき、力の作用点を通って力の方向に引いた直線を、力の作用線といいます。
また、力の作用している物体を剛体(外力を受けても変形を無視できる物体)と見なすことができるとき、力の作用線は、力の作用線上であれば任意の点に移動しても力の作用効果は変わりません。
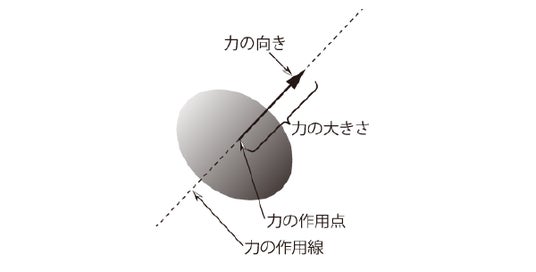
【図1:力の表現】
2. 力の合成と分解
力の合成とは、物体に多くの力が作用するとき、これらの力と等しい効果を持つ1つの力を求めることをいいます。そして力の合成によって求めた力を、合力といいます。一方、力の分解とは、1つの力をこれと効果が等しいいくつかの力に分けることをいいます。
また、力の分解によって分けられた力を、分力といいます。
力の合成や分解は、いくつかの力がある1点に作用している場合は、比較的容易に求めることができます。図式解法で求める力の平行四辺形と示力図、数式解法で求める直交座標系による力の分解と合成を説明します。
・力の平行四辺形
力の平行四辺形とは、2つ以上の力で描ける平行四辺形のことで、その対角線が合力となります。
合力は、力の平行四辺形を用いて示します。図2は、力の平行四辺形を用いた求め方です。
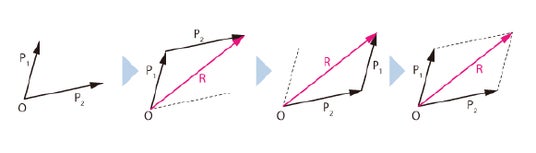
【図2:力の平行四辺形】
同一平面内にある力を、平面力といいます。図2の左に示すように、ある1点(O点)を作用点にする2つの平面力P1とP2が存在するとしましょう。
ここで、図2の左から2番目に示すように、P2の作用点(始点)をP1の矢印の先(終点)に移動します。また、P1の始点とP2の終点とを結ぶ直線を描いて、P2の終点側に矢印を描きます。
描いた平面力Rは、平面力P1とP2の合力です。
合力Rは、その次の図に示すように、P2の終点にP1の始点を移動させても同様に求めることができます。従って、図2の右に示すように、平行四辺形を描くことで合力Rは求められます。
・示力図
示力図とは、複数の力をつなぎ、力の始点と終点を結んで合力を示した図のことです。
図3は、示力図を用いた求め方です。
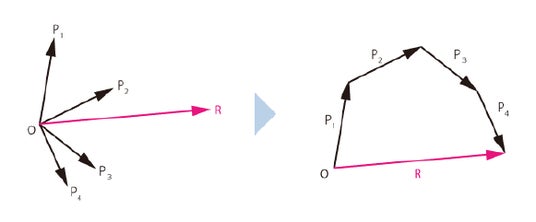
【図3:示力図】
力の平行四辺形や示力図は、図式解法と呼ばれる方法です。
ただし、この方法では作図する力の数に限界があります。
また、作図中に誤差を生じてしまいます。そこで、直交座標軸を用います。
・直交座標系による力の分解と合成
直交座標軸とは、互いに直交するx軸、y軸、z軸の3軸から構成される座標系のことです。
ここでは、平面力を考えていますので、2軸で構成される直交座標軸を用いて、原点Oを作用点とするいくつかの平面力をx座標軸の分力とy座標軸の分力に分けます。
このとき、図4の左に示すように、x軸と角度θを成す平面力Pのx方向の分力はPcosθ、y方向の分力はPsinθで表すことができます。
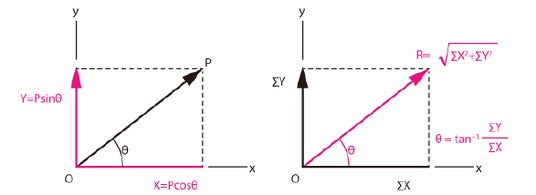
【図4:直交座標系による力の分解と合成】
全ての力の分力を求めれば、x方向の分力やy方向の分力は、それぞれ単純に足したり引いたりすることができます。それぞれの分力の総和を求めた後に三平方の定理を用いれば、図4の右に示すように、これらの力の合力を求めることができます。
また、合力の方向とx軸との成す角度は、逆三角関数を用いて求めることができます。
これを数式解法といいます。
3. モーメント
モーメントとは、物体に回転を生じさせるような力の性質を表します。図5に示すように、物体に力Pが作用して、ある1点Oを中心に円運動(物体の回転)を起こしたとしましょう。
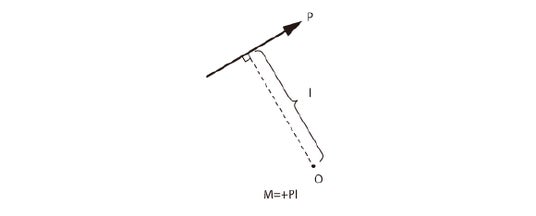
【図5:モーメント】
ある点を回転させる能力(モーメント)の大きさは、力Pとある点から作用線まで垂線である距離との積で表されます。すなわち、図5の場合、モーメントの大きさMは、M=P×lになります。
もし、力の向きが反対であれば、モーメントの大きさは負の符号を用いてM=-P×lと表します。
なお、通常は時計回りを正、反時計回りを負と決めて問題を解きます。
モーメントに関する、バリニオンの定理と偶力のモーメントの2つについて説明します。
・バリニオンの定理
バリニオンの定理とは、一般に任意の1点に関する多くの力のモーメントの総和は、これらの合力が同じ点に関して引き起こすモーメントの大きさに等しいことを示します(図6)。
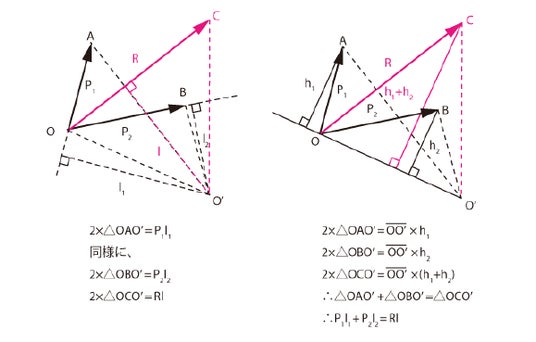
【図6:バリニオンの定理】
・偶力のモーメント
偶力とは、物体に2つの平面力が作用するとき、これら2つの力の大きさが等しく、かつ方向が反対向きで、その作用線が平行な1組の力をいいます。
偶力は、1つに合成することができず、物体を移動させる働きはないものの、物体を回転させる働き(モーメント)があります。
図7に示すように、偶力のモーメントは一定の値になります。
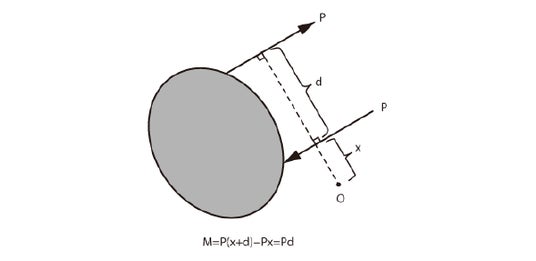
【図7:偶力のモーメント】
いかがでしたか?
今回は、力の合成と分解、モーメントについて紹介しました。
次回は、建築構造物のモデル化を解説します。お楽しみに!
続きはDLしてご覧ください
企業プレスリリース詳細へ
PRTIMESトップへ

